MAFALDA

A Benchmark and Comprehensive Study of Fallacy Detection and Classification


Chadi Helwe¹	Tom Calamai²	Pierre-Henri Paris¹	Chloé Clavel²	Fabian Suchanek¹

Goals

Performance: SOTA LLMs and humans on fallacy detection and classification?

Benchmark: unification public existing fallacy collections
Taxonomy: covers existing dataset
Annotation Scheme: to tackle subjectivity

A fallacy is an erroneous or invalid way of reasoning.

“You must either support my presidential candidacy or be against America!”

This argument is a false dilemma fallacy: it wrongly assumes no other alternatives.

Why bother with fallacies?

The Witch Hunts in Europe and North America (15th-18th Centuries): The witch hunts were fueled by a combination of the bandwagon fallacy, where the widespread acceptance of witchcraft as truth spurred further persecutions, and the ad hominem fallacy, attacking individuals’ character or circumstances rather than addressing the actual evidence of witchcraft.
The Tulip Mania (1637): Often considered the first recorded speculative bubble, the tulip mania was partially driven by the bandwagon fallacy, with investors believing they must invest because others were doing so, and the appeal to probability fallacy, assuming that prices would continue to rise simply because they had done so in the past.
The Dreyfus Affair (1894-1906): This political scandal in France was significantly influenced by confirmation bias and scapegoating, where Alfred Dreyfus was wrongly accused and convicted of treason largely due to preexisting prejudices against his Jewish heritage.
The Domino Theory and the Vietnam War (1955-1975): The domino theory, which suggested that if one country in a region came under the influence of communism, then the surrounding countries would inevitably follow, was a form of slippery slope fallacy. This reasoning contributed to the U.S. decision to escalate its involvement in Vietnam, leading to a prolonged and costly conflict.
McCarthyism (1950s): Senator Joseph McCarthy’s campaign against alleged communists in the US government and other institutions was partly based on the guilt by association fallacy, where individuals were accused and persecuted not based on concrete evidence but on their supposed associations or sympathies with communist organizations.

First things first, some definitions

Argument

An argument consists of an assertion called the conclusion and one or more assertions called premises, where the premises are intended to establish the truth of the conclusion. Premises or conclusions can be implicit in an argument.

Fallacy

A fallacy is an argument where the premises do not entail the conclusion.

Taxonomies of Fallacies

What about taxonomies in current works on fallacy annotation, detection, and classification?

lack of consistency across the different dataset:

different granularity
different coverage
some are hierachical, others are not

Our taxonomy aims to systematize and classify those fallacies that are used in current works.

Level 0 is a binary classification
Level 1 groups fallacies into Aristotle’s categories:
- Pathos (appeals to emotion),
- Ethos (fallacies of credibility),
- and Logos (fallacies of logic, relevance, or evidence).
Level 2 contains fine-grained fallacies within the broad categories of Level 1.

Accompanying the taxonomy, we provide both formal and informal definitions for each fallacies.

An example

“Why should I support the 2nd Amendment, do I look like toothless hick?”

Appeal to ridicule

This fallacy occurs when an opponent's argument is portrayed as absurd or ridiculous with the intention of discrediting it.

$E_1$ claims $P$. $E_2$ makes $P$ look ridiculous, by misrepresenting $P$ ($P$'). Therefore, $\neg P$

Disjunctive Annotation Scheme

In the last New Hampshire primary election, my favorite candidate won. Therefore, he will also win the next primary election.

Is it:

a false causality?
a causal oversimplification?

The argument goes that the candidate has to win again because he won last time. This can be seen as a false causality fallacy: a cause-effect relationship is incorrectly inferred between two events that have nothing to do with each other.

However, it can also be seen as a causal oversimplification fallacy. This is because we can contend that having won the last election gives the candidate an edge over other candidates in terms of visibility, and thus makes it more likely that he wins this year’s election as well. The argument is thus fallacious mainly because it fails to acknowledge other factors that play a role in re-election.

It would be counter-productive if the annotators converged on, say, causal oversimplification, so that every approach of fallacy annotation is penalized for proposing an (equally plausible) false causality.

Legitimately differing opinions

One annotator may see implicit assertions that another annotator does not see.
- “Are you for America? Vote for me!”
Annotators may also have different thresholds for fear or insults.
Different annotators have different background knowledge.
- “Use disinfectants or you will get Covid-19!”

Let “$a\ b\ c\ d$” be a text where $a$, $b$, $c$, and $d$ are sentences.

$S= ${$a\ b, d$}, “$a\ b$” has labels {$l_1, l_2$}, and “$d$” has label {$l_3$}.

In that case, $G=${ $(a\ b,$ {$l_1, l_2$}$) , (d, ${$l_3$}$)$ }

An example of prediction could be

$P=${$(a, l${$l_1$}$), (a, ${$l_2$}$), (b, ${$l_3$}$), (c, ${$l_4$}$), (d, ${$l_1$}$)$}

A text is a sequence of sentences $st_1, \ldots, st_n$.

The span of a fallacy in a text is the smallest contiguous sequence of sentences that comprises the conclusion and the premises of the fallacy. If the span comprises a pronoun that refers to a premise or to the conclusion, that premise or conclusion is not included in the span.

Let $\mathcal{F}$ be the set of fallacy types and $\bot$ be a special label which means “no fallacy”. Given a text and its set of spans $S$ (possibly overlapping), then the gold standard $G$ of a text is the set of pairs of all $s \in S$, along with their respective alternative labels, represented as follows:
$G \subseteq S \times \mathcal{P}(\mathcal{F}\cup${$\bot$}$)\setminus${$\emptyset, ${$\bot$}}

Given a text and its segmentation of (possibly overlapping) spans $S$, then a prediction $P$ of the text is a set of pairs of all $s \in S$ paired with exactly one predicted label, represented as follows:
$P\subseteq S \times \mathcal{F}\cup{\bot}$

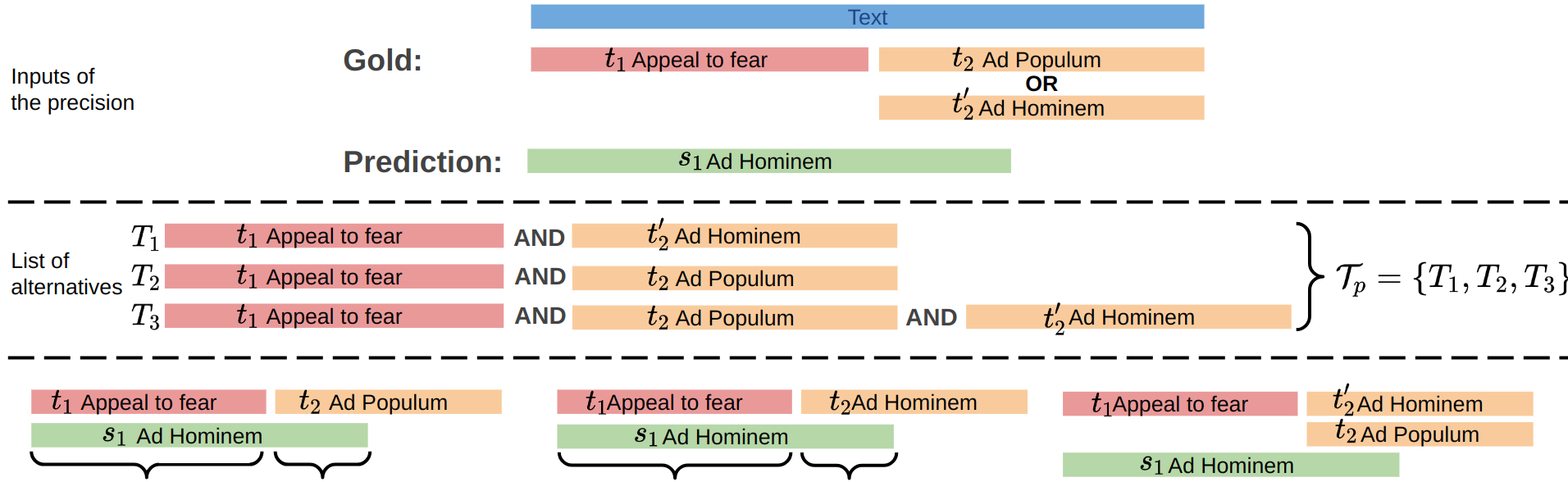
Comparison score

$C(p, l_p, g, l_g, h) = \frac{|p \cap g|}{h} \times \delta(l_p, l_g)$
$\delta(x,y)=[x \cap y \neq \emptyset]$

$\textit{Precision}(P, G)=\frac{\sum\limits_{(p, l_p)\in P}\max\limits_{(g, l_g)\in G} C(p, l_p, g, l_g, |p|)}{|P|}$
If $|P|=0$, then $\textit{Precision}(P, G)=1$

$\textit{Recall}(P, G)=\frac{\sum\limits_{(g, l_g)\in G^-}\max\limits_{(p, l_p)\in P}C(p, l_p, g, l_g, |g|)}{|G^-|}$
If $|G^-|=0$, then $\textit{Recall}(P, G)=1$

The MAFALDA dataset

Multi-level Annotated FALlacy DAtaset

English-language corpus of 9,745 texts:

News outlets: Martino et al. (2019)¹
- γ = 0.26 $\rightarrow$ γ = 0.60
Reddit: Sahai et al. (2021)²
- Cohen’s κ = 0.515
Online quizzes and climate-related texts from news outlets: Jin et al. (2022)³
American political debates: Goffredo et al. (2022)⁴
- Krippendorff’s α = 0.5439

Disagreements are interpreted as noise, and are removed with various strategies.

Annotating

Why re-annotating?

Lack of consistency between taxonomies
Annotations scheme variations
Variations in the way consensus is achieved

$\rightarrow$ We manually re-annotated from scratch 200 randomly selected texts

Manual re-annotation, from scratch, of 200 randomly selected texts from our merged corpus
Our sample mirrors the distribution of sources and the original labels in our corpus
LLMs and crowd workers were not involved (33%-46% of Mturk workers are estimated to use ChatGPT (Veselovsky et al., 2023))

Re-annotation process

The authors discussed each text together

identifying each argument in a text
determining whether it is fallacious
determining the span of the fallacy
choosing the fallacy type(s)

We discussed each fallacious span together, and either converged on one annotation or permitted several alternative annotations for the same span. We provide an explanation for each annotation, and we provide a completed template for each annotation

More concretely, a span is identified and classified as follows: (i) identifying each argument in a text, (ii) determining whether it is fallacious, (iii) determining the span of the fallacy (as defined in Definition 4.2), and (iv) choosing the fallacy type(s). When disagreement occurs, the group discusses the discrepancy and must agree on a final span and list of fallacies (including the “no fallacy” label).

The process took around 40 hours. This corresponds to an average of 12 minutes per example, ranging from less than a minute for toy examples to half an hour when disagreement raised a debate. The total number of person-hours was 130.

Performance results

	MAFALDA
Model	F1 Level 0	F1 Level 1	F1 Level 2
Baseline random	0.435	0.061	0.010
Falcon	0.397	0.130	0.022
LLAMA2 Chat	0.572	0.114	0.068
LLAMA2	0.492	0.148	0.038
Mistral Instruct 7B	0.536	0.144	0.069
Mistral 7B	0.450	0.127	0.044
Vicuna 7B	0.494	0.134	0.051
WizardLM 7B	0.490	0.087	0.036
Zephyr 7B	0.524	0.192	0.098
LLaMA2 Chat 13B	0.549	0.160	0.096
LLaMA2 13B	0.458	0.129	0.039
Vicuna 13B	0.557	0.173	0.100
WizardLM 13B	0.520	0.177	0.093
GPT 3.5 175B	0.627	0.201	0.138
Avg. Human	0.749	0.352	0.186

User annotations as gold standard

Gold Standard	F1 Level 0	F1 Level 1	F1 Level 2
User 1	0.616	0.310	0.119
User 2	0.649	0.304	0.098
User 3	0.696	0.253	0.093
User 4	0.649	0.277	0.144
MAFALDA	0.749	0.352	0.186

Conclusion

MAFALDA is a unified dataset designed for fallacy detection and classification
A new taxonomy of fallacies
A new annotation scheme that embraces the subjectivity
LLMs in zero-shot fallacy detection and classification at the span level
Human evaluation

Future work

Extension to few-shot settings
Advanced prompting techniques
Enriching the dataset
Model fine-tuning
Top-down approach

Da San Martino, G., Seunghak, Y., Barrón-Cedeno, A., Petrov, R., & Nakov, P. (2019). Fine-grained analysis of propaganda in news article. ↩︎
Sahai, S., Balalau, O., & Horincar, R. (2021, August). Breaking down the invisible wall of informal fallacies in online discussions. ↩︎
Jin, Z., Lalwani, A., Vaidhya, T., Shen, X., Ding, Y., Lyu, Z., … & Schölkopf, B. (2022). Logical fallacy detection. ↩︎
Goffredo, P., Haddadan, S., Vorakitphan, V., Cabrio, E., & Villata, S. (2022, July). Fallacious argument classification in political debates. ↩︎