
Introduction to Machine Learning
Supervised Learning - Linear Models
Introduction to Supervised Learning
What is Supervised Learning?
- A type of machine learning where the model learns from labeled data.
- Input data: Features (X), Output: Target labels (y).
- Common tasks:
- Regression: Predicting continuous values (e.g., house prices).
- Classification: Predicting categories (e.g., spam detection).
- 🎯 Find a function that maps inputs to outputs.

Simplified Workflow
of Supervised Learning
- Data collection and preprocessing.
- Model training with labeled data.
- Model evaluation and validation.
- Deployment for predictions on unseen data.
- Importance of clean, normalized, and labeled datasets for effective learning.
- Scaling ensures all features contribute equally and improves optimization convergence.
Data Preparation
Data Preprocessing
- Preprocessing ensures data is clean and suitable for machine learning models.
- Why preprocess data?
- Improves model convergence and stability.
- Prevents features with large ranges from dominating others.
- Ensures compatibility with algorithms sensitive to feature scaling.
- Common preprocessing steps:
- Handle missing values (e.g., imputation).
- Encode categorical features (e.g., one-hot encoding).
- Feature Scaling: Critical for many algorithms. (See next slide for details.)

Feature Scaling
- Why scale features?
- Ensures all features contribute equally to the model.
- Improves convergence speed for gradient descent.
- Prevents features with large ranges from dominating others.
- Methods:
- Normalization: Rescales data to [0, 1].
- Formula: $x' = \frac{x - min(x)}{max(x) - min(x)}$
- Used for neural networks and distance-based models.
- Standardization: Centers data to mean 0 and scales to unit variance.
- Formula: $x' = \frac{x - \mu}{\sigma}$
- Used for regression, SVMs, and PCA.
- Normalization: Rescales data to [0, 1].
- When to use:
- Normalization: For models sensitive to absolute ranges.
- Standardization: For models sensitive to variance.
Numerical Stability
- Why it matters:
- Prevents overflow or underflow in computations.
- Ensures reliable training and evaluation of models.
- Techniques for stability:
- Clipping values: Limit inputs to functions (e.g.,
np.clipfor sigmoid). - Log-sum-exp trick: Stabilizes logarithmic computations.
- Avoid division by zero: Add small values ($\epsilon$) to denominators.
- Clipping values: Limit inputs to functions (e.g.,
- Example: Sigmoid function
- Without clipping: Risk of overflow for large inputs.
- With clipping: Inputs limited to a safe range.

import numpy as np
def sigmoid_with_clipping(x):
# Clip input values to [-5, 5] range for numerical stability
x_clipped = np.clip(x, -5, 5)
# Apply sigmoid function
return 1 / (1 + np.exp(-x_clipped))
# Example usage
x = np.array([-10, -5, 0, 5, 10])
y = sigmoid_with_clipping(x)
print(f"Input: {x}")
print(f"Output: {y}")
# Output: [0.00669285 0.00669285 0.5 0.99330715 0.99330715]Linear Regression
Introduction to Linear Regression
- Regression predicts continuous values.
- Linear regression finds the relationship between features ($X$)
and
target ($y$): \[ y = Xw + b \] - Examples:
- Predicting house prices based on size, location, etc.
- Forecasting stock prices.

Cost Function for Linear Regression
- The cost function measures how well the model fits the data.
- For linear regression, use Mean Squared Error (MSE): \[ \text{MSE} = \frac{1}{N} \sum_{i=1}^{N} \left( y_i - \hat{y}_i \right)^2 \]
- Smaller MSE means a better fit.
- Regularization: Adds a penalty term to the cost function to control model
complexity:
- Prevents overfitting by penalizing large weights.
- Common types: L1 (Lasso), L2 (Ridge).

Optimization with Gradient Descent
- Gradient descent minimizes the cost function.
- Update rules for weights (w) and bias (b): \[ w := w - \eta \nabla_w \text{Cost}, \quad b := b - \eta \nabla_b \text{Cost}\quad \text{ where } \nabla_w \text{Cost} = \begin{bmatrix}\frac{\partial \text{Cost}}{\partial w_1} \\\frac{\partial \text{Cost}}{\partial w_2} \\\vdots \\\frac{\partial \text{Cost}}{\partial w_n}\end{bmatrix}.\]
- $\eta$: Learning rate (step size).
- Gradient clipping: Limits the magnitude of gradients to stabilize training.
- Early stopping: Halts training when loss improvement becomes negligible.

Regularization
Regularization
- Helps prevent overfitting by adding a penalty term to the cost function.
- Types of regularization:
- L1 (Lasso): Encourages sparse models by penalizing absolute weights.
- L2 (Ridge): Penalizes the square of the weights for smoother models.
- Impact on optimization:
- L1: Adds a constant gradient penalty proportional to the sign of weights.
- L2: Adds a gradient penalty proportional to the magnitude of weights.
- Regularized cost functions:
- L1: $\text{Cost} + \lambda \sum |w|$
- L2: $\text{Cost} + \lambda \sum w^2$

Logistic Regression
Introduction to Logistic Regression
- Used for binary classification tasks (e.g., spam vs. non-spam).
- Maps input features to a probability value using the sigmoid function: \[ \sigma(z) = \frac{1}{1 + e^{-z}}, \quad z = Xw + b \]
- Output is a probability between 0 and 1.
- Decision boundary separates classes (e.g., 0.5 for binary classification).

Loss Function for Logistic Regression
- Uses binary cross-entropy loss to evaluate model performance: \[ \text{Loss} = - \frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right] \]
- Minimizes the distance between predicted probabilities and true labels.
- Penalty increases for incorrect predictions.

Decision Boundaries
- A decision boundary is a line or surface that separates different classes.
- For logistic regression, the boundary is linear.
- Examples:
- 2D classification: A line separating two classes.
- Higher dimensions: A hyperplane.

Model Tuning
Hyperparameter Tuning
- What are hyperparameters?
- Settings chosen before training the model (e.g., learning rate, regularization strength).
- Do not change during training, unlike model parameters (weights, biases).
- Why tune hyperparameters?
- Improves model performance and generalization.
- Avoids underfitting and overfitting.
- Common approaches:
- Grid Search: Try all combinations of specified values.
- Random Search: Sample random combinations within a range.
- Manual Tuning: Adjust based on intuition and results.
- Example: Tuning learning rate and $\lambda$ for regularization.
Cross-Validation
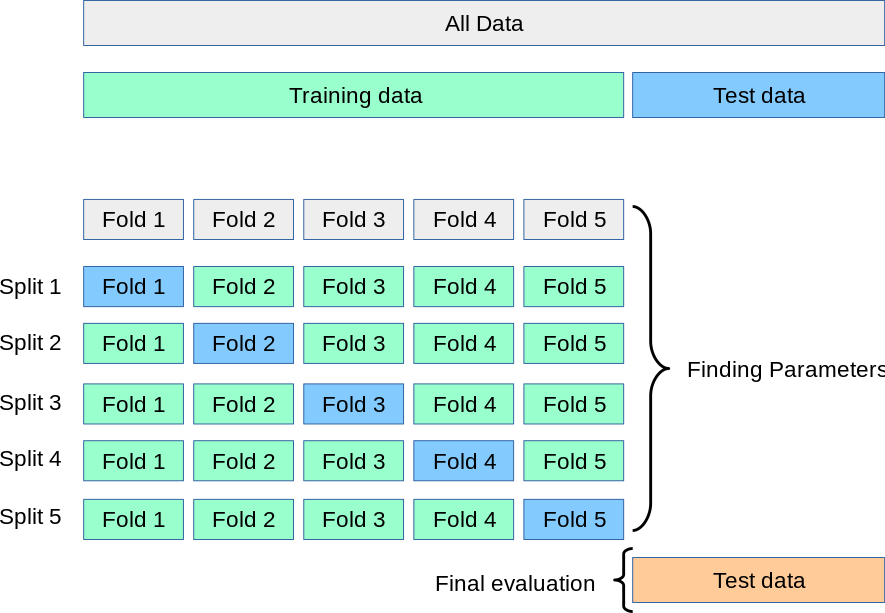
- Ensures robust evaluation by splitting data into training and validation sets.
- k-Fold Cross-Validation:
- Splits data into k subsets (folds).
- Trains the model on k-1 folds and validates on the remaining fold.
- Repeats k times and averages the performance.
- Reduces risk of overfitting to a single validation set.
Model Evaluation
Regression Metrics
- Common metrics for evaluating regression models:
- Mean Squared Error (MSE): Average of squared differences between actual and predicted values.
- Root Mean Squared Error (RMSE): Square root of MSE for interpretability in original units.
- R2-score: Proportion of variance explained by the model.
- Regularization impact:
- May increase MSE slightly but improves generalization.
- R² should still remain high for a well-regularized model.
| Metric | Formula | Without Regularization | With Regularization | Interpretation |
|---|---|---|---|---|
| MSE | $\frac{1}{n} \sum_{i=1}^{n} \left( y_i - \hat{y}_i \right)^2$ | 24.5 | 26.8 | Lower is better. Slightly increases with regularization due to bias-variance tradeoff. |
| RMSE | $\text{RMSE} = \sqrt{\text{MSE}}$ | 4.95 | 5.18 | Interpretable in original units. Shows actual average prediction error magnitude. |
| R²-score | $1 - \frac{\text{MSE}}{\text{Var}(y)}$ | 0.98 | 0.96 | Proportion of variance explained (0-1). Should remain high with proper regularization. |
| Note: Example values shown for a typical housing price prediction model. Actual values will vary by dataset and model. | ||||
Classification Metrics
- Metrics to evaluate binary classifiers:
- Accuracy: Percentage of correct predictions.
- Precision: Ratio of true positives to predicted positives.
- Recall: Ratio of true positives to actual positives.
- F1-Score: Harmonic mean of precision and recall.
- Use a confusion matrix to visualize predictions.

Advanced Concepts
Bias-Variance Tradeoff
- Bias: Error from incorrect model assumptions (e.g., underfitting).
- Variance: Error from sensitivity to small changes in the training data (e.g., overfitting).
- Tradeoff:
- Low bias → More complex model, higher variance.
- Low variance → Simpler model, higher bias.
- 🎯 Find the optimal balance for best performance.

Debugging Tips
- Common issues:
- Vanishing gradients: Use appropriate learning rates and activation functions.
- Overfitting: Add regularization or use cross-validation.
- Poor scaling: Normalize or standardize features to improve model performance.
- Numerical instability:
- Clip values (e.g., gradients or sigmoid inputs) to prevent overflow or underflow.
- Adjust initialization of weights for better stability.
- Exploding gradients: Apply gradient clipping to limit their magnitude.
- Solutions:
- Tune hyperparameters (e.g., learning rate, regularization strength) iteratively.
- Analyze model performance with evaluation metrics and loss curves.
Recap
- Linear Regression:
- Predicts continuous values.
- Optimized using gradient descent and evaluated with metrics like MSE and R².
- Logistic Regression:
- Used for binary classification tasks.
- Outputs probabilities, uses sigmoid function, and evaluated with metrics like accuracy and F1-score.
- Regularization:
- Prevents overfitting by penalizing large coefficients (L1/L2).
- Evaluation:
- Metrics for regression and classification guide model improvements.